Ogive
In ballistics or aerodynamics, an ogive is a pointed, curved surface mainly used to form the approximately streamlined nose of a bullet, shell, missile or aircraft.
The traditional or secant ogive is a surface of revolution of the same curve that forms a Gothic arch; that is, a circular arc, of greater radius than the diameter of the cylindrical section ("shank"), is drawn from the edge of the shank until it intercepts the axis.
If this arc is drawn so that it meets the shank at zero angle (that is, the distance of the centre of the arc from the axis, plus the radius of the shank, equals the radius of the arc), then it is called a tangential or spitzer ogive. This is a very common ogive for high velocity (supersonic) rifle bullets.
The sharpness of this ogive is expressed by the ratio of its radius to the diameter of the cylinder; a value of one half being a hemispherical dome, and larger values being progressively more pointed. Values of 4 to 10 are commonly used in rifles, with 6 being the most common.
Another common ogive for bullets is the elliptical ogive. This is a curve very similar to the spitzer ogive, except that the circular arc is replaced by an ellipse defined in such a way that it meets the axis at exactly 90°. This gives a somewhat rounded nose regardless of the sharpness ratio. An elliptical ogive is normally described in terms of the ratio of the length of the ogive to the diameter of the shank. A ratio of one half would be, once again, a hemisphere. Values close to 1 are common in practice. Elliptical ogives are mainly used in pistol bullets.
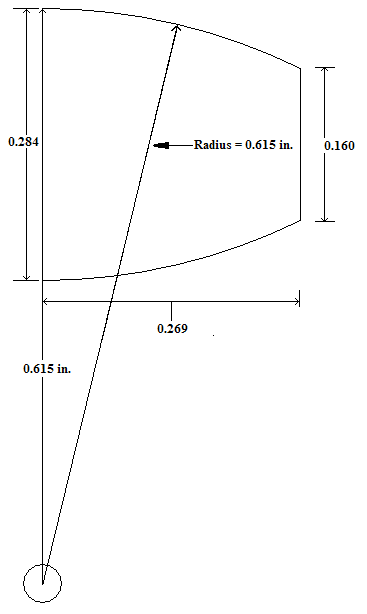
Tangent Ogive
A tangent ogive is an arc of a circle that meets the bullet body contour smoothly, creating a smooth transition where the ogive joins the cylindrical body. The center of rotation of the arc lies in the plane of the base of the nose.
The dimensions of a Tangent Ogive may be defined by 4 dimensions: The radius of the curve, the length of the nose, the base diameter and the tip diameter. If any three of the dimensions are known, the fourth may be calculated using the algorithms defined below.
For the calculations that follow, remember that:
|
|
Radius of the ogive: R = Sqr( L ) / ( D – T ) + ( D – T ) / 4
R1 = Sqr( L )
R2 = R1 / ( D – T )
R = R2 + ( D – T ) / 4
Length of the ogive: L = SqRt( R * ( D - T ) - Sqr( D - T ) / 4 )
L1 = Sqr( D - T )
L2 = L1 / 4
L3 = R * ( D - T ) - L2
L = SqRt( L3 )
Diameter of the ogive tip: T = D - 2 * R + SqRt( 4 * ( Sqr( R ) - Sqr( L ) )
T1 = Sqr( R ) - Sqr( L )
T2 = SqrRt( T1 * 4)
T = D - 2 * R + T2
Diameter of the ogive base: D = T + 2 * R - SqRt( 4 * ( Sqr( R ) - Sqr( L ) )
D1 = Sqr( R ) - Sqr( L )
D2 = SqrRt( D1 * 4)
D = T + 2 * R - D2