Difference between revisions of "Bullet drop"
(New page: Bullet drop for a [[M4 and M16 rifle]] '''Bullet drop''' is the name given to the tendency of a [[...) |
m (1 revision) |
Latest revision as of 15:24, 15 March 2013
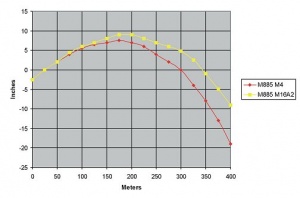
Bullet drop is the name given to the tendency of a bullet to drop in flight due to the effect of gravity. It is important to understand the ballistics of a given cartridge when zeroing the weapon. For example, Hornady lists a bullet drop of 42.40 in (1.076 m) at a distance of 500 yards (457.2 m) for a .30-06 rifle zeroed at 200 yards (182.88 m).[1] To plan for bullet drop and compensate properly, one must understand the parabolic trajectory of the round. Once the rifle is calibrated to hit the desired mark at a given range, one can estimate where the round will be at any point along its trajectory (with the exception of windage, which is a lateral movement, as opposed to the vertical movement of bullet drop). After the trajectory is plotted, one can use a bullet drop compensator (or "BDC") to adjust the rifle without the need to fire a shot.
In general, smaller bullets, such as the .204 Ruger and .17 HMR are more prone to bullet drop and wind drift due to the lower ballistic coefficient (BC).
Many ballistics tables show a rise in trajectory at distances shorter than the one used for sight-in. This apparent "rise" of the bullet in the first part of its trajectory is relative only to the sighting plane, and is not actually a rise. The laws of physics dictate that the projectile will begin to be pulled down by gravity as soon as it leaves the support of the muzzle, and can never rise above the axis of the barrel. The apparent "rise" is caused by the separation of the plane of the sighting device and that of the barrel. This separation distance can be as much as 2-inches with some optical sighting systems. If a firearm is zeroed at 100 meters, then the sighting plane and the projectile path must intersect at that distance; the sighting plane must be adjusted to "cross" the projectile path at 100 meters. In the case of a barrel that is maintained in a perfectly horizontal position, the sighting device must be inclined downward to achieve this intersection. The height of the sighting device above the barrel axis dictates the amount of angular declination required to achieve the required intersection. Due to the parabolic shape of the projectile path, the sighting plane will cross the bullet's trajectory at two points, causing part of the bullet path to appear to rise above the flat sighting plane. The distance at which the firearm is zeroed, and the height of the sighting device above the barrel axis, determine the apparent severity of the "rise" in both the X and Y axes (how far above the sighting plane the rise goes, and over what distance it lasts).